Anche se a priori sembra non esserci alcun motivo valido per cui i tombini debbano essere rotondi, la motivazione c'è ed è anche essenziale per chi ci lavora: i tombini rotondi non possono cadere in un buco rotondo che stanno ricoprendo!
Per capire il perché, proviamo a pensare ad un tombino quadrato, come quello in figura.
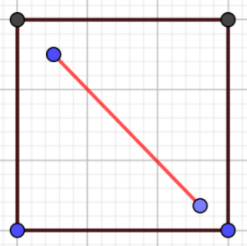
Se si prende il coperchio quadrato (la linea rossa in figura) e lo si prova ad inserire nel buco lungo la diagonale, sarà facile farlo cadere. Questa stessa proprietà - ossia che esiste un modo per far cadere il coperchio dentro al tombino - vale per gran parte delle figure note, fra cui i triangoli.
Tuttavia il cerchio non è l'unica figura per cui ciò non accade. Le figure adatte "ad essere dei tombini" sono dette figure a spessore costante - dove appunto lo spessore, che intuitivamente è la distanza fra due punti del bordo "opposti", rimane sempre uguale. Più rigorosamente - lo spessore di una figura lungo una direzione - è la minima distanza fra le due rette parallele, ortogonali alla direzione, che contengono interamente la figura.
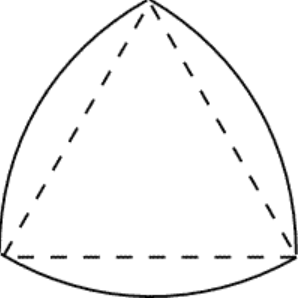
Una delle più famose è il triangolo di Reuleaux, illustrato nella figura qui sotto.