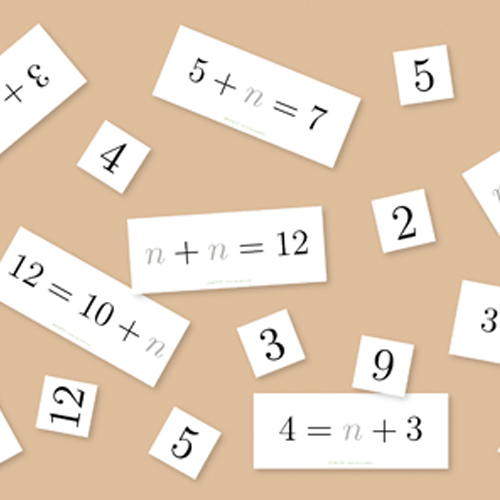

Scheda Tecnica
CLASSI: terza, quarta e quinta.
Competenze Indicazioni Nazionali:
L'alunno:
- riconosce e risolve problemi in contesti diversi valutando le informazioni e la loro coerenza;
- spiega il procedimento seguito, anche in forma scritta, mantenendo il controllo sia sul processo risolutivo, sia sui risultati;
- confronta procedimenti diversi e produce formalizzazioni che gli consentono di passare da un problema specifico a una classe di problemi.
METODOLOGIE E STRATEGIE:
Il percorso chiede di trovare soluzioni di equazioni e di semplici disequazioni. Non si applicano le tecniche classiche dell’algebra, ma si procede per tentativi. Procedere per tentativi significa arrivare gradualmente ad una soluzione, senza penalizzare gli errori. Nella pratica didattica, l’errore è spesso associato al fallimento perché l’insegnamento è a volte visto come addestramento e dunque basato su procedimenti riproducibili (Zan & Di Martino, 2017). Ma evitare l'errore limita la possibilità di apprendimento dialogico, basato sul confronto tra verità e falsità. Ricerche recenti hanno mostrato che l'introduzione di esercizi completati appositamente in modo errato a fianco di esercizi corretti faciliti l’apprendimento degli studenti (Rushton, 2018). In questo percorso, l’approccio per tentativi costringe la classe a cercare una strategia per arrivare più rapidamente alla soluzione, cosa che favorisce la comprensione dell'argomento.
Il percorso è stato ideato da Luigi Bernardi, Giorgia Damiano.
-
attività
- Il numero segreto
- Pensa un numero


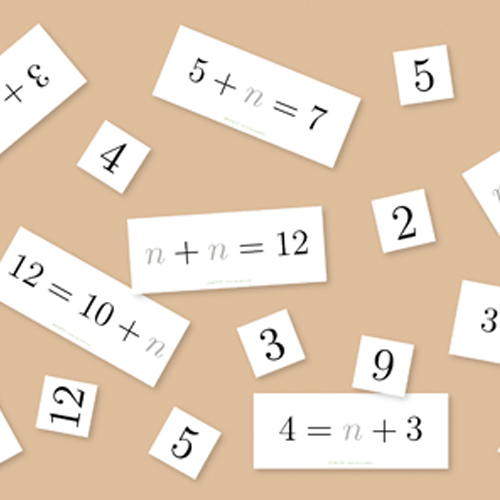

-
attività
- Il numero segreto
- Pensa un numero
Scheda Tecnica
CLASSI: terza, quarta e quinta.
Competenze Indicazioni Nazionali:
L'alunno:
- riconosce e risolve problemi in contesti diversi valutando le informazioni e la loro coerenza;
- spiega il procedimento seguito, anche in forma scritta, mantenendo il controllo sia sul processo risolutivo, sia sui risultati;
- confronta procedimenti diversi e produce formalizzazioni che gli consentono di passare da un problema specifico a una classe di problemi.
METODOLOGIE E STRATEGIE:
Il percorso chiede di trovare soluzioni di equazioni e di semplici disequazioni. Non si applicano le tecniche classiche dell’algebra, ma si procede per tentativi. Procedere per tentativi significa arrivare gradualmente ad una soluzione, senza penalizzare gli errori. Nella pratica didattica, l’errore è spesso associato al fallimento perché l’insegnamento è a volte visto come addestramento e dunque basato su procedimenti riproducibili (Zan & Di Martino, 2017). Ma evitare l'errore limita la possibilità di apprendimento dialogico, basato sul confronto tra verità e falsità. Ricerche recenti hanno mostrato che l'introduzione di esercizi completati appositamente in modo errato a fianco di esercizi corretti faciliti l’apprendimento degli studenti (Rushton, 2018). In questo percorso, l’approccio per tentativi costringe la classe a cercare una strategia per arrivare più rapidamente alla soluzione, cosa che favorisce la comprensione dell'argomento.
Il percorso è stato ideato da Luigi Bernardi, Giorgia Damiano.
Julia Robinson
 Julia Robinson è stata una matematica americana, che si è occupata di logica matematica, teoria delle equazioni, teoria degli algoritmi e teoria dei giochi.
Julia Robinson è stata una matematica americana, che si è occupata di logica matematica, teoria delle equazioni, teoria degli algoritmi e teoria dei giochi.
Da bambina, per motivi di salute perse due anni di scuola; ma, in un solo anno, riuscì a recuperare il tempo perduto. Successivamente prese il Dottorato sotto la guida di Alfred Tarski, uno dei più noti logici matematici in quel periodo.
Julia Robinson ha poi insegnato matematica, logica e statistica all’Università della California, nella prestigiosa sede di Berkeley.
Nella sua vita, ha ricevuto molti riconoscimenti. In particolare, nel 1982 è stata Presidente dell’American Mathematical Society, la società scientifica che riunisce tutti i matematici degli Stati Uniti.
Morì a causa di una leucemia.
Il risultato più importante di Julia Robinson è legato al “problema di decisione” per certe equazioni. Nella scuola secondaria noi studiamo come si risolvono le equazioni di primo e di secondo grado. È facile rendersi conto che, anche se consideriamo un’equazione in cui tutti i coefficienti sono interi, può capitare che le soluzioni non siamo intere (basta pensare a 2x = 1 oppure x2 = 5).
D’altra parte, in molte situazioni pratiche hanno interesse soltanto le soluzioni intere. Per esempio, in certi problemi si chiede il numero di persone che partecipano a una festa, o il numero di camion necessari per un certo trasporto (in questi problemi capita talvolta che uno studente, senza ragionare troppo, risponda 3,5 camion!).
Pensiamo ora a equazioni con più di un’incognita, come x3 – 2y2 = 5 o anche a equazioni più lunghe e complicate. Non è troppo difficile trovare una soluzione dell’equazione considerata: attribuisco ad x un valore a mia scelta, per esempio pongo x = 3; dopo di che, con qualche passaggio, trovo che y =√11. Ma... c’è una soluzione dove sia x sia y siano interi? Non conosco formule come nel caso delle equazioni di secondo grado; posso solo procedere per tentativi. In questo caso, sono fortunato perché c’è una soluzione con numeri non troppo grandi: x = 7 ed y = 13. Infatti, 73 – 2×132 = 5.
Tuttavia, in generale, procedere per tentativi è pericoloso, perché si corre il rischio di continuare per molto tempo senza trovare nulla. Quando ci si ferma? E poi, se ci si ferma e si rinuncia, resta il dubbio di aver interrotto i tentativi proprio nel momento sbagliato, perché stavamo per arrivare a una soluzione.
Nel 1900 il grande matematico David Hilbert pose esplicitamente il problema (noto come decimo problema di Hilbert): trovare un procedimento generale che, data un’equazione, permetta di stabilire se esiste almeno una soluzione intera.
Il problema è estremamente difficile e si arrivò ad una soluzione solo nel 1970. A questa soluzione collaborarono quattro grandi matematici: Martin Davis, Yuri Matiyasevich, Hilary Putnam e, appunto, Julia Robinson (per cui qualcuno parla del teorema DMPR). E, contrariamente a quanto si poteva sperare, la soluzione è “negativa”: il procedimento generale richiesto da Hilbert non esiste! Anche avendo a disposizione i migliori computer del mondo, non si potrà mai progettare un software che permetta di stabilire se un’equazione ammette o no soluzioni intere (un procedimento si può trovare solo se ci si limita a particolari tipi di equazioni).
Due osservazioni importanti. In primo luogo, il risultato è frutto della collaborazione di quattro studiosi, ciascuno dei quali ha dato un contributo essenziale. Difficilmente un unico studioso, per quanto geniale, sarebbe riuscito ad arrivare alla soluzione da solo.
E poi il risultato, come dicevamo, è negativo. La matematica è spesso vista come la materia in cui si calcola, si risolve, si dimostra; ma perfino la matematica ha i suoi limiti. E la logica matematica, in qualche caso, è riuscita a precisare proprio questi limiti: ci sono problemi (come quello considerato) che nessuno potrà mai risolvere. Può sembrare scoraggiante. In realtà, un risultato “negativo” è spesso molto fecondo, perché apre la strada a successive ricerche, sempre più approfondite e affascinanti.