ZERMELO GAME è un gioco online per favorire la comprensione e l’uso consapevole delle espressioni tutti, almeno uno, nessuno. L'obiettivo del gioco è realizzare più punti possibile in un tempo prestabilito rispondendo opportunamente alle domande che vengono mostrate.
Nella pagina iniziale si seleziona con quali quantificatori giocare (si possono anche selezionare entrambi), l'ambiente - cioè quali tipi di oggetti compariranno a schermo (colori, poligoni, numeri o sacchi) -, il livello e il tempo a disposizione nella partita. Si possono inoltre selezionare le modalità negazione e testimone che vedremo in seguito.
I livelli e gli ambienti di gioco sono da intendersi in uno sviluppo progressivo delle competenze. L'ambiente poligoni richiede competenze anche nel nucleo tematico spazio&figure, l'ambiente numeri nel nucleo tematico numeri, mentre gli ambienti colori e sacchi si riferiscono unicamente al nucleo tematico logica.
- Quantificatore TUTTI
Il giocatore deve capire se tutti o non tutti gli elementi di un certo insieme godano di una certa proprietà (scritta in alto).
Nell'esempio in figura la risposta corretta è NON TUTTI, perché non tutte le palline dell'insieme sono verdi.
-
Quantificatore ALMENO UNO
Il giocatore deve capire se almeno uno o nessuno degli elementi di un certo insieme goda di una certa proprietà.
Nell'esempio in figura la risposta corretta è ALMENO UNO, perché almeno una delle figure mostrate è un triangolo.
COLORI
Nell'ambiente colori, compaiono a schermo palline che possono essere colorate di rosso, verde o blu. Le proprietà che compaiono in alto sono ROSSO, VERDE, BLU.
POLIGONI
LIVELLO 1
Gli elementi che compaiono sono poligoni (cioè figure piane delimitate da segmenti) e le proprietà sono TRIANGOLO, QUADRILATERO, PENTAGONO, ESAGONO (non compaiono invece poligoni con più di 6 lati).
LIVELLO 2
Nel livello 2, oltre alle proprietà del livello 1, viene introdotta la proprietà EQUILATERO. Un poligono si dice equilatero se ha tutti i lati uguali. Analogamente, un poligono non è equilatero se ha almeno una coppia di lati diversi.
Ricordiamo che un quadrilatero equilatero viene comunemente chiamato rombo (dal gr. rhómbos che vuol dire trottola).
LIVELLO 3
Nel livello 3, oltre alle proprietà del livello 1 e 2, vengono introdotte le proprietà ALMENO DUE ANGOLI UGUALI, ALMENO DUE LATI UGUALI, UN ANGOLO RETTO, UN ANGOLO OTTUSO. Le proprietà "un angolo retto" e "un angolo ottuso" sono da intendersi come "il poligono ha almeno un angolo retto/ottuso". Molto spesso, infatti, l'espressione "almeno uno" è sottointesa nel linguaggio.
Le proprietà "almeno due angoli uguali" e "almeno due lati uguali" compaiono riferite esclusivamente a triangoli. Si noterà con la classe che le proprietà sono equivalenti: un triangolo ha almeno due lati uguali se e solo se ha almeno due lati uguali. Un triangolo del genere viene chiamato comunemente isoscele (dal greco isoskelḗs, dove ísos vuol dire uguale e skélos vuol dire lato).
LIVELLO 4
A partire dal livello 4, i pulsanti di risposta variano leggermente, dando più spazio al simbolismo: in particolare al posto dell'espressione tutti compare esclusivamente il simbolo ∀ e al posto dell'espressione almeno uno compare esclusivamente il simbolo ∃. Ricordiamo che il simbolo ∀ deriva dall'inglese ALL (cioè, appunto, tutti) mentre il simbolo ∃ dall'inglese EXISTS (cioè esiste, almeno uno).
Nel livello 4, oltre alle proprietà precedenti, viene introdotta la proprietà ALMENO DUE LATI PARALLELI.
Per un triangolo è impossibile avere due lati paralleli, mentre un quadrilatero con almeno due lati paralleli viene usualmente chiamato trapezio (dal greco trapézion cioè piccola tavola).
LIVELLO 5
Il livello 5 aggiunge le proprietà EQUIANGOLO e REGOLARE. Un poligono si dice equiangolo quando ha tutti gli angoli uguali mentre regolare quando è sia equiangolo che equilatero.
Un quadrilatero equiangolo viene comunemente chiamato rettangolo (perché se un quadrialtero ha tutti gli angoli uguali ha di conseguenza tutti gli angoli retti), mentre un quadrilatero regolare (che è cioè sia un rettangolo sia un rombo) viene comunemente chiamato quadrato.
NUMERI
LIVELLO 1
Nel livello 1 di numeri, compaiono i numeri compresi fra 1 e 9 e le proprietà PARI e DISPARI.
Un numero è pari quando esiste un numero che sommato con sé stesso dà il numero di partenza. Ad esempio, 10 è pari perché 10 = 5 + 5, mentre 0 è pari perché 0 = 0 + 0. Un numero che non è pari è dis-pari. Infatti il prefisso dis, in italiano, è usato per negare la parola che segue: non essere ordinati vuol dire essere dis-ordinati, essere a dis-agio vuol dire non essere a proprio agio.
LIVELLO 2
Nel livello 2, oltre alle proprietà deli livello 1, compaiono anche MAGGIORE e MINORE. In questo caso sono presenti numeri fino a 100.
LIVELLO 3
Nel livello 3, oltre le proprietà precedenti, compaiono anche le proprietà DIVISIBILE PER 3, DIVISIBILE PER 4, DIVISIBILE PER 5 e ULTIMA CIFRA.
SACCHI
In quest'ambiente compaiono per la prima volta i quantificatori alterianti: il giocatore deve considerare frasi come "tutti i sacchi contengono almeno una pallina blu" oppure "almeno un sacco ha tutte le palline blu", cioè frasi con due quantificatori.
Prendiamo in considerazione la situazione seguente.
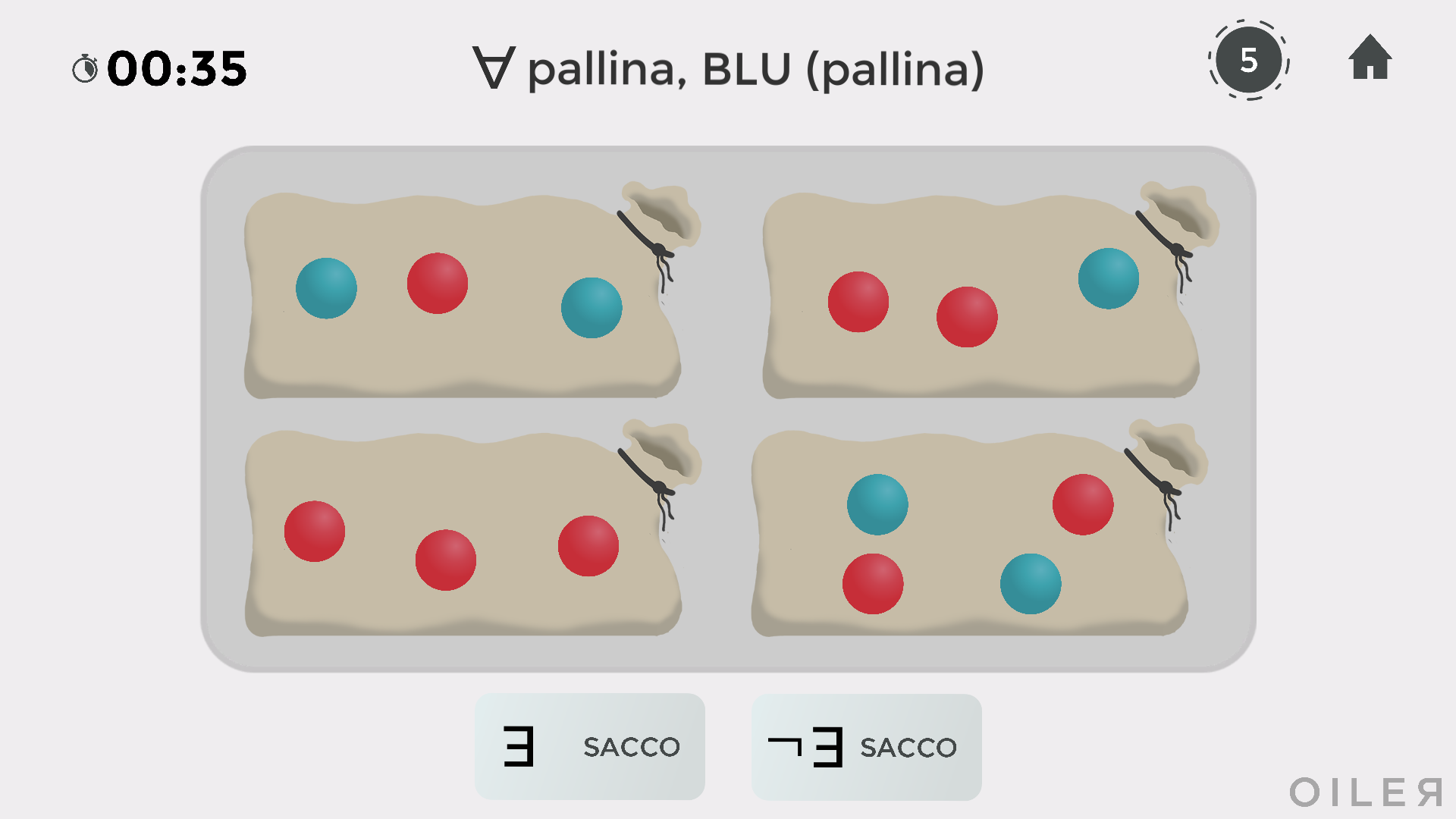
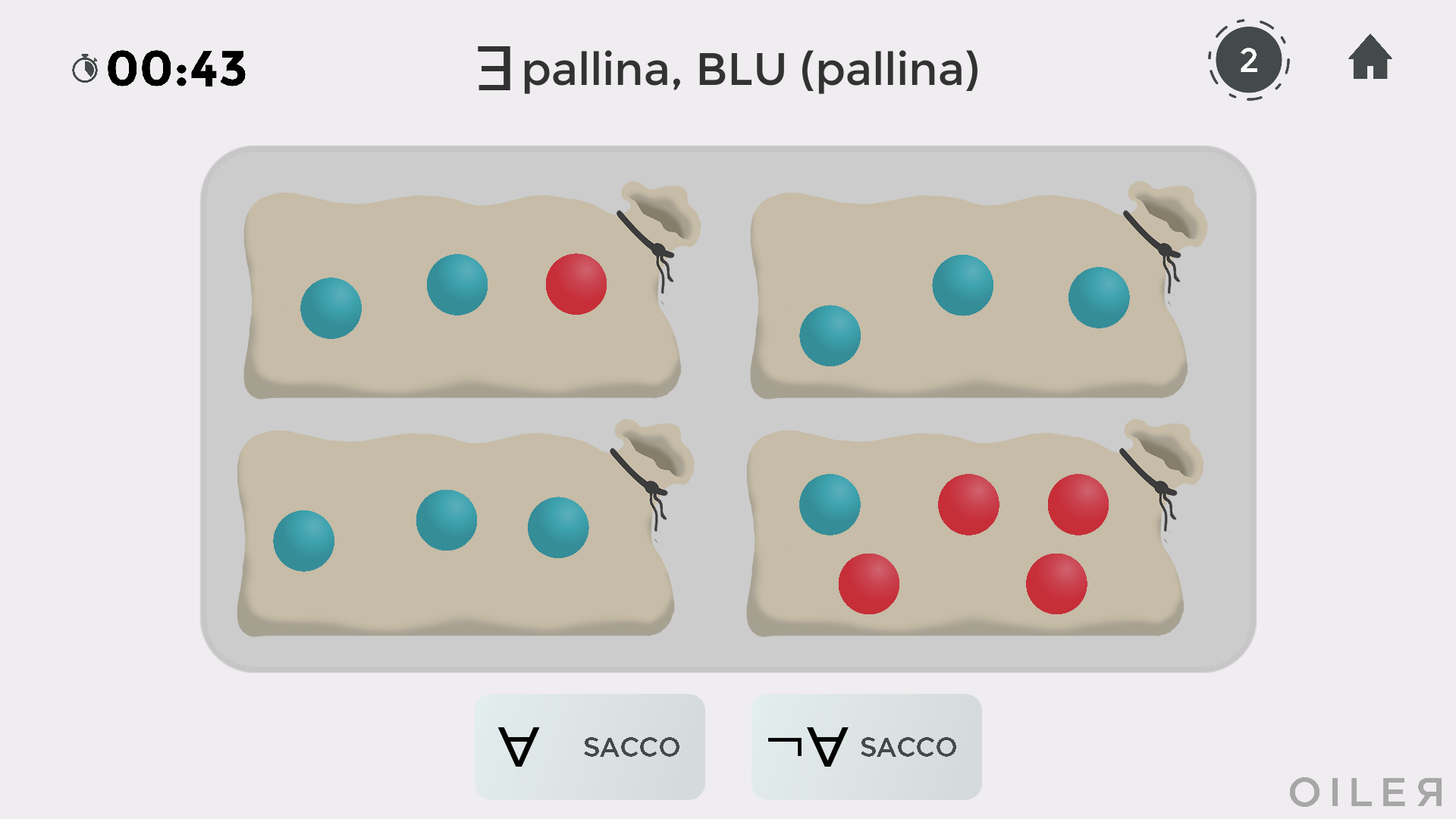
In alto compare la proprietà da riferire ai singoli sacchi ∀ pallina, BLU(pallina), da leggersi come "per ogni pallina, quella pallina è blu" oppure "tutte le palline sono blu". La notazione BLU(pallina) fa riferimento a quanto introdotto nel percorso di BUL.
In basso si chiede se esiste o meno un sacco con questa proprietà, cioè un sacco che abbia tutte le palline blu. La risposta è negativa e quindi bisogna fare click sul pulsante "¬ ∃ SACCO".
Come secondo esempio, consideriamo la situazione seguente.
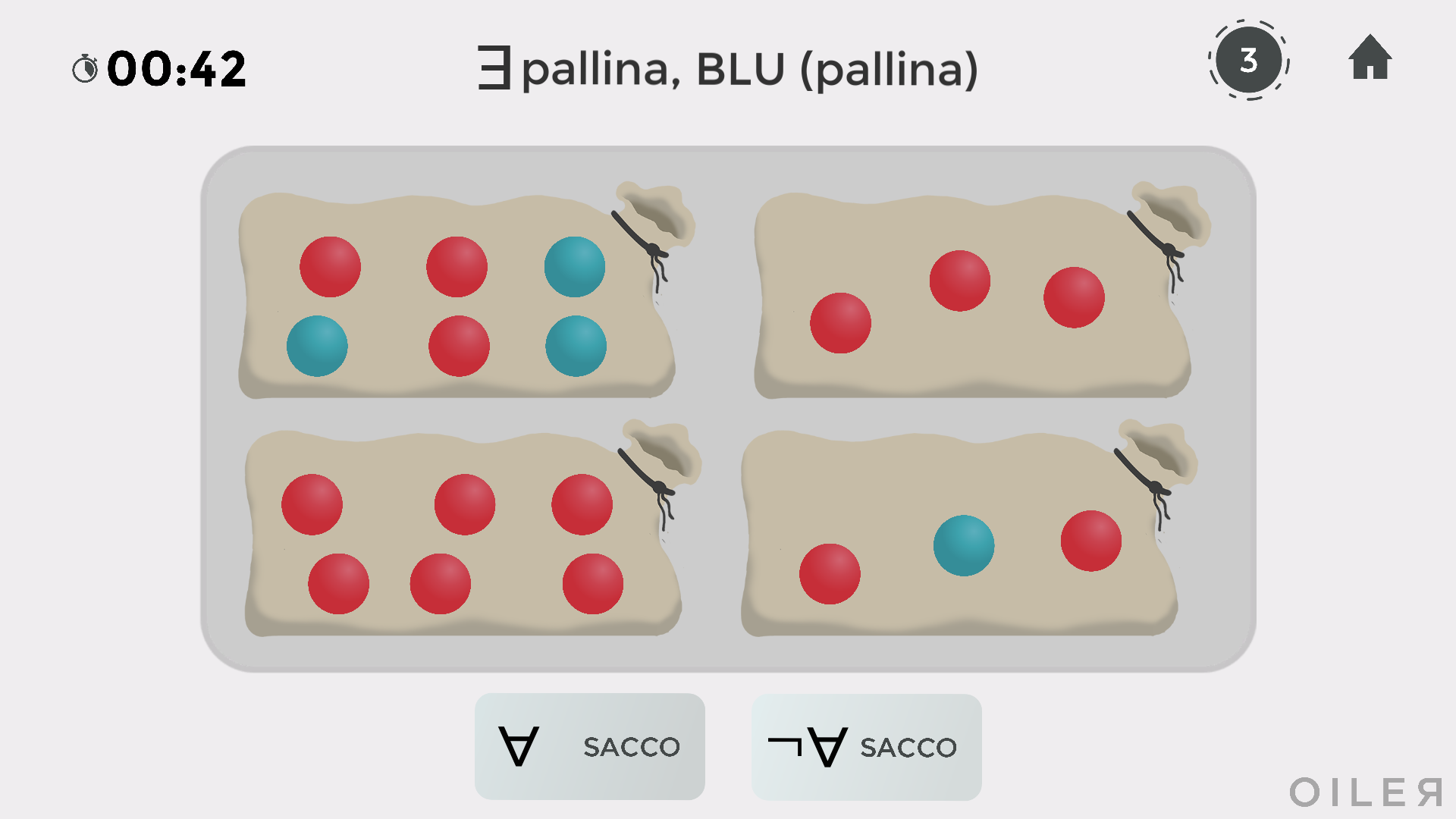
In alto compare la proprietà da riferire ai singoli sacchi ∃ pallina, BLU(pallina), da leggersi come "esiste una pallina blu" oppure "almeno una pallina è blu".
In basso si chiede se tutti o non tutti i sacchi verifichino questa proprietà, cioè se tutti i sacchi contengano almeno una pallina blu. La risposta è negativa e quindi bisogna fare click sul pulsante "¬ ∀ SACCO".
MODALITÀ TESTIMONE
Se nella pagina iniziale si selezione la Modalità Testimone si aggiunge una nuova regola.
Quando si fa click su "non tutti" oppure su "almeno uno" (cioè quando si dà una risposta esistenziale) bisogna fornire un testimone, cioè indicare un oggetto che testimoni la scelta fatta.
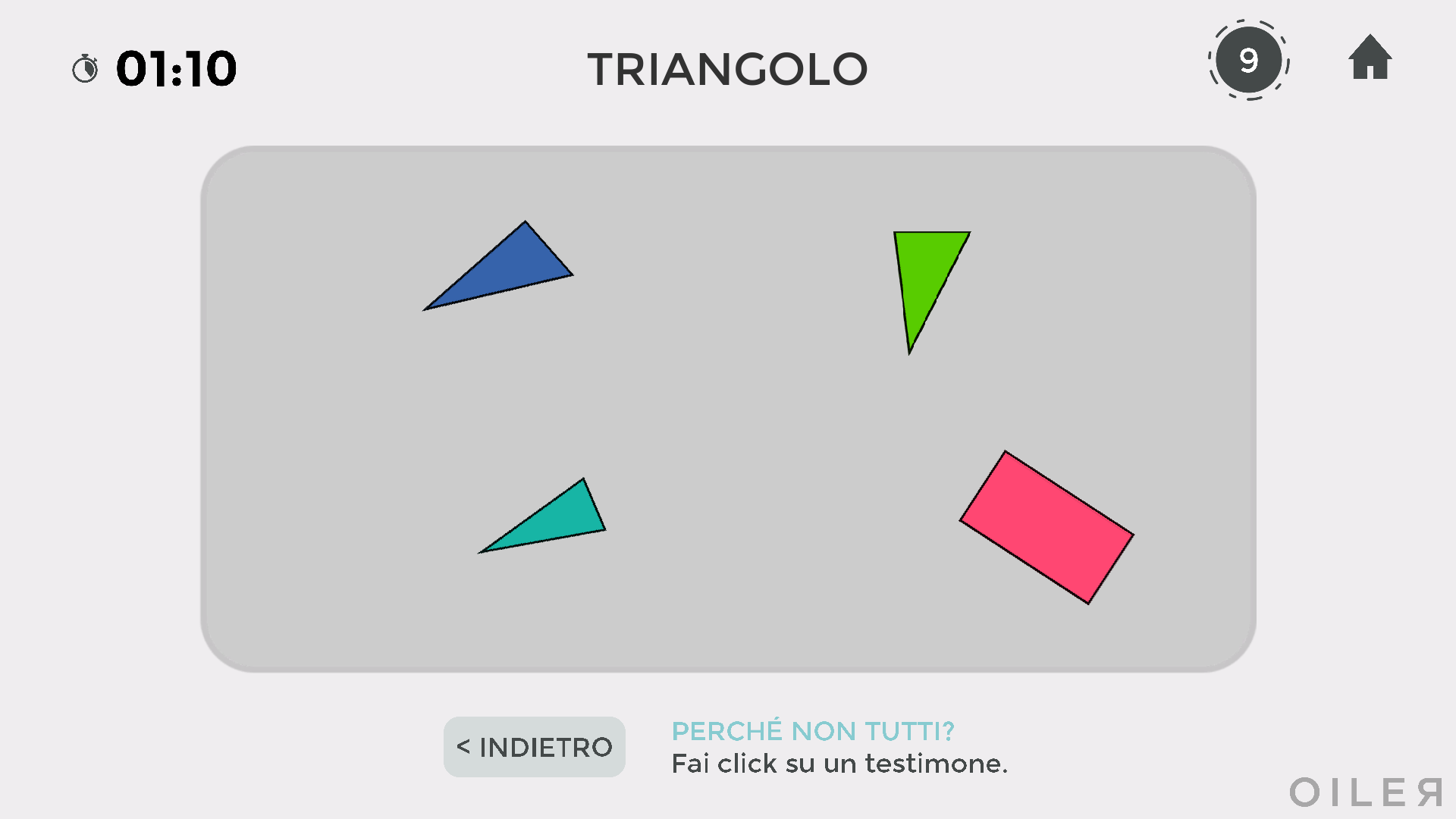
Nel caso del "non tutti" è richiesto di fare click su un oggetto che non goda della proprietà indicata. Ad esempio, facendo riferimento alla figura seguente, dopo aver fatto click su "non tutti", bisogna selezionare un poligono che non sia un triangolo, in questo caso il rettangolo rosa.
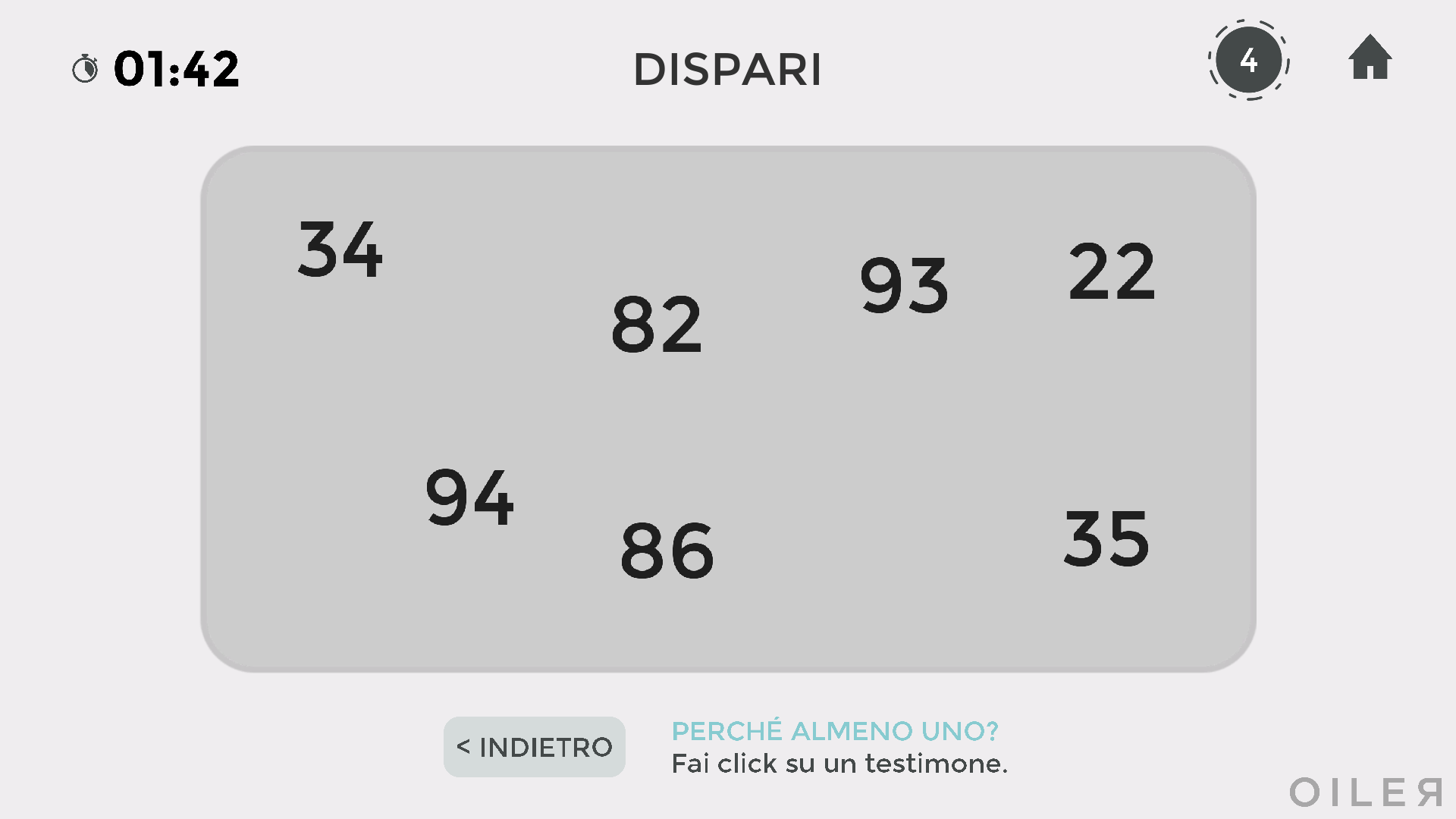
Similmente, nel caso di "almeno uno" è richiesto di fare click su un oggetto che goda della proprietà indicata. Ad esempio, facendo riferimento alla figura seguente, dopo aver fatto click su "almeno uno", bisogna selezionare un numero dispari, in questo caso 93 oppure 35.
SACCHI E MODALITÀ TESTIMONE
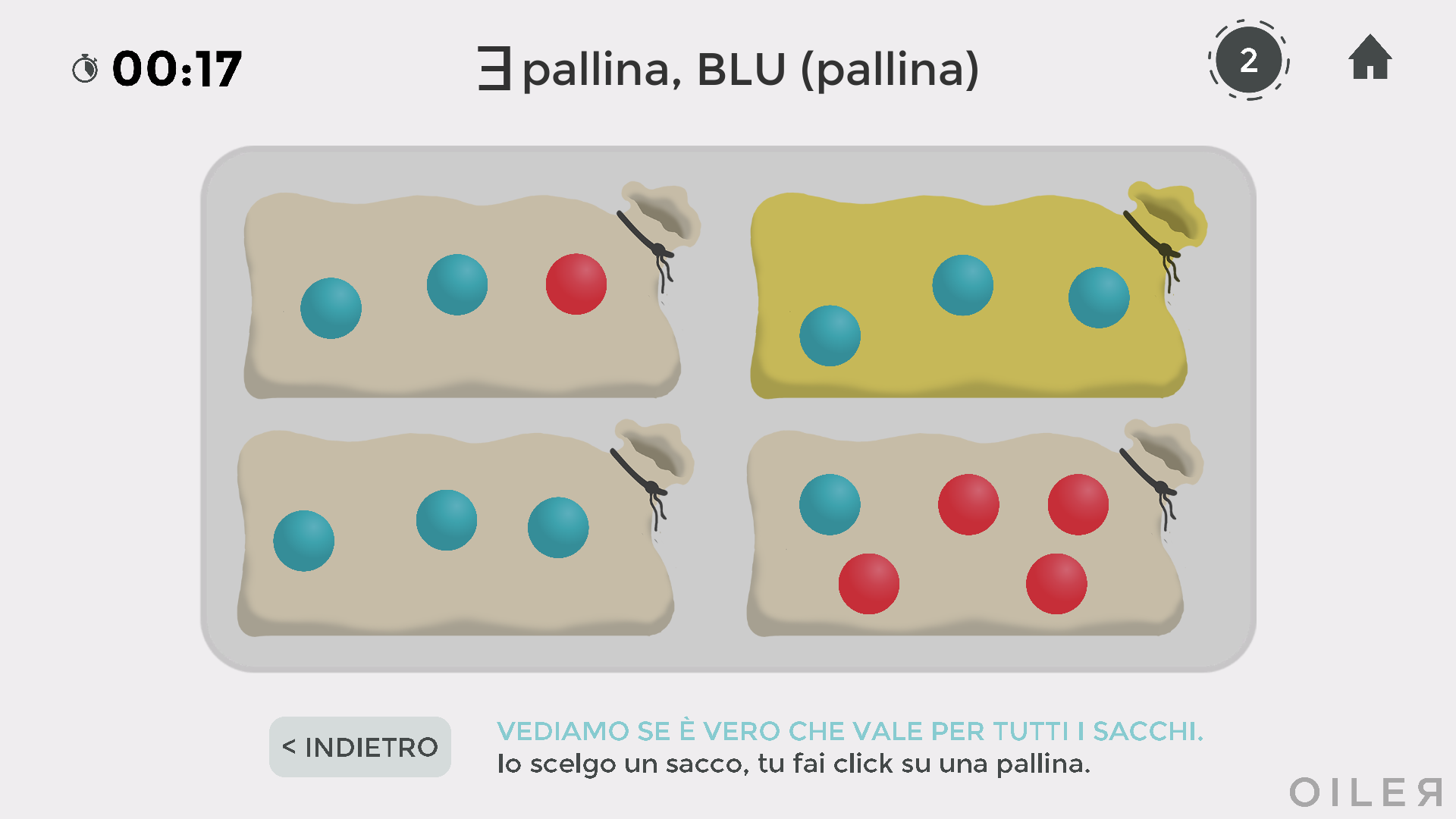
La modalità testimone nell'ambiente sacchi - pur seguendo lo stesso principio presentato sopra - è più complessa: in questo caso, avviene un vero e proprio dialogo fra giocatore e PC. Per capire meglio la situazione, facciamo un esempio.
Se si sostiene che in tutti sacchi ci sia almeno una pallina blu, allora - comunque il PC sceglierà un sacco - si sarà in grado di individuare una pallina blu in quel sacco.
Riportiamo di seguito alcune possibilità a titolo di esempio:
- se si sostiene che tutti i sacchi abbiano tutte le palline rosse, non bisogna fare alcunché (0 click totali);
- se si sostiene che non tutti i sacchi abbiano tutte le palline rosse, bisogna fare click su un sacco dove almeno una pallina è blu, quindi fare click su una pallina blu (2 click totali);
- se si sostiene che almeno un sacco abbia tutte le palline rosse, bisogna fare click sul sacco con tutte le palline rosse (1 click totale, fatto sul sacco);
- se si sostiene che tutti i sacchi abbiano almeno una pallina rossa, bisogna fare click su una pallina rossa in un sacco scelto dal PC (1 click totale, fatto su una pallina).
MODALITÀ NEGAZIONE
Se si seleziona modalità negazione, allora - in alto - oltre alle normali proprietà compariranno anche queste proprietà ma negate. Il simbolo ¬ va appunto letto come "non".
Ad esempio, essere ¬ VERDE vuol dire "non essere verde", quindi - nel caso del gioco - o rosso o blu. Analogamente, essere ¬ PARI vuol dire "non essere pari", cioè dispari.
Facendo riferimento alla situazione seguente, viene chiesto se almeno una pallina sia non blu, quindi rossa o verde.
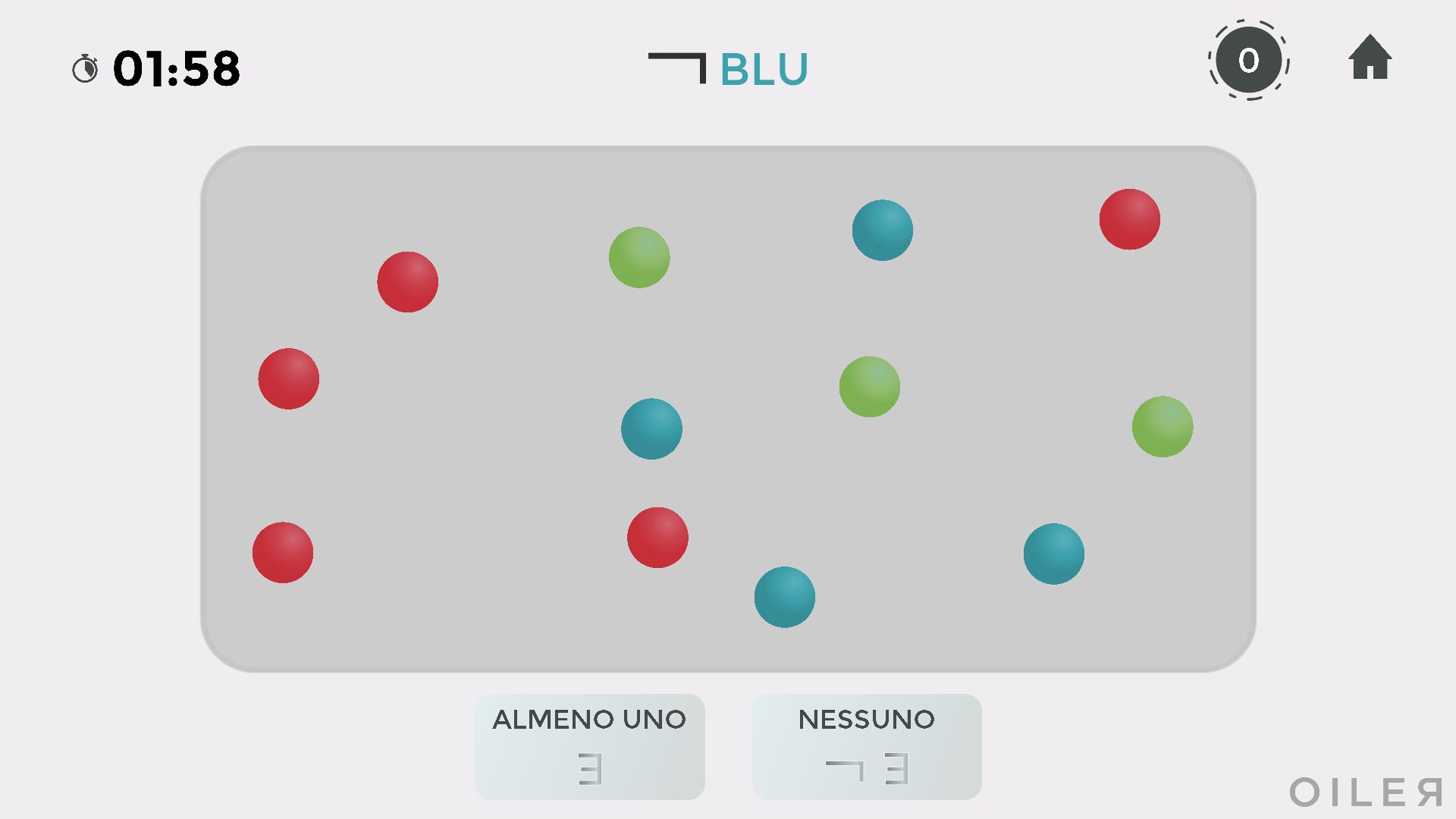
La risposta è chiaramente affermativa. Se si sta giocando anche con la modalità testimone, si procederà quindi a fare click su una pallina rossa o verde.
Vale la pena sottolineare il - non semplice - caso mostrato in figura.
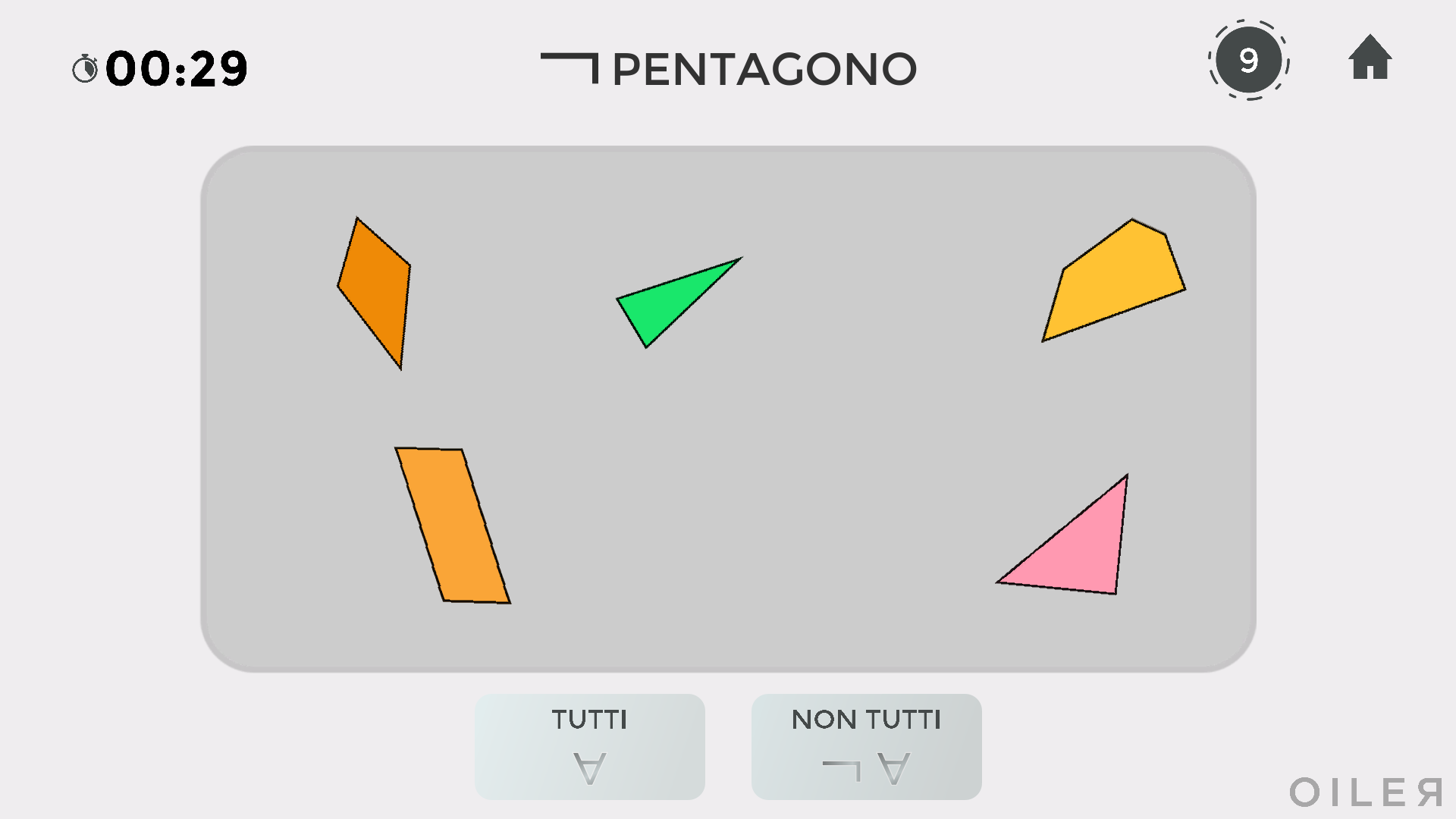
Essere "non pentagono" vuol dire - nel contesto del gioco - essere triangolo, quadrilatero oppure esagono. In figura quindi non tutti sono non pentagoni, perché il poligono giallo in alto a destra ha effettivamente 5 lati. Se si sta giocando con la modalità testimone, bisognerà fare click proprio sul pentagono.