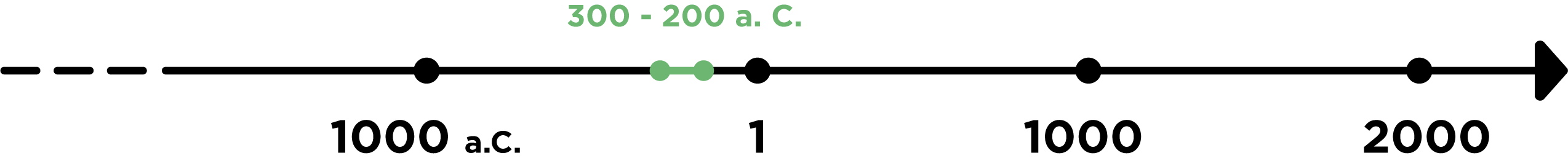PINGO è un percorso didattico rivolto alla scuola primaria per introdurre alla probabilità. Le attività proposte ruotano intorno ad artefatti manipolativi di uso corrente: urne, monete, dadi e carte. Il percorso consolida l’uso dei numeri decimali e promuove un approccio alle frazioni. All'interno del percorso si affrontano anche scommesse e gioco d’azzardo. Riteniamo fondamentale che si parli di gioco d’azzardo nelle scuole dal punto di vista matematico: si tratta di illustrare ai futuri cittadini le quotazioni e i meccanismi su cui si basano le scommesse e – di conseguenza – far capire come e perché non è conveniente giocare d’azzardo. In sintesi, riteniamo che un cittadino consapevole dal punto di vista matematico riesca più facilmente a valutare i rischi legati a gratta&vinci, Lotto, SuperEnalotto, sale corse, macchinette e a tutte quelle situazioni in cui vengono proposte scommesse inique.

Scheda Tecnica

DURATA COMPLESSIVA MEDIA DEL PERCORSO: 12 ore

CLASSI: terza, quarta e quinta.

Competenze Indicazioni Nazionali:
L'alunno:

  • ricerca dati per ricavare informazioni e costruisce rappresentazioni (tabelle e grafici);
  • riconosce e quantifica, in casi semplici, situazioni di incertezza;
  • riconosce e utilizza rappresentazioni diverse di oggetti matematici (numeri decimali, frazioni, percentuali, scale di riduzione, ...);
  • costruisce ragionamenti formulando ipotesi, sostenendo le proprie idee e confrontandosi con il punto di vista di altri.

METODOLOGIE E STRATEGIE:
Il percorso proposto si basa su un approccio sia quantitativo sia qualitativo alla probabilità, coinvolgendo la nozione di frequenza. La psicologia cognitiva suggerisce il termine frequenza naturale (Hoffrage et al., 2002) per indicare un rapporto non espresso da frazioni o percentuali, ma descritto attraverso situazioni concrete, che coinvolga un’azione di estrazione o suddivisione e sia dunque intuitivo. L’uso di frequenze naturali in combinazione con materiali pratici e coinvolgenti rende accessibili agli studenti della scuola primaria concetti e contenuti probabilistici (Till e Sproesser, 2020). Questo consente un successivo passaggio verso l’astrazione e il concetto di frazione.

Il percorso è stato ideato da Luigi Bernardi, Dario Domingo.
PINGO è un percorso didattico rivolto alla scuola primaria per introdurre alla probabilità. Le attività proposte ruotano intorno ad artefatti manipolativi di uso corrente: urne, monete, dadi e carte. Il percorso consolida l’uso dei numeri decimali e promuove un approccio alle frazioni. All'interno del percorso si affrontano anche scommesse e gioco d’azzardo. Riteniamo fondamentale che si parli di gioco d’azzardo nelle scuole dal punto di vista matematico: si tratta di illustrare ai futuri cittadini le quotazioni e i meccanismi su cui si basano le scommesse e – di conseguenza – far capire come e perché non è conveniente giocare d’azzardo. In sintesi, riteniamo che un cittadino consapevole dal punto di vista matematico riesca più facilmente a valutare i rischi legati a gratta&vinci, Lotto, SuperEnalotto, sale corse, macchinette e a tutte quelle situazioni in cui vengono proposte scommesse inique.

Scheda Tecnica

DURATA COMPLESSIVA MEDIA DEL PERCORSO: 12 ore

CLASSI: terza, quarta e quinta.

Competenze Indicazioni Nazionali:
L'alunno:

  • ricerca dati per ricavare informazioni e costruisce rappresentazioni (tabelle e grafici);
  • riconosce e quantifica, in casi semplici, situazioni di incertezza;
  • riconosce e utilizza rappresentazioni diverse di oggetti matematici (numeri decimali, frazioni, percentuali, scale di riduzione, ...);
  • costruisce ragionamenti formulando ipotesi, sostenendo le proprie idee e confrontandosi con il punto di vista di altri.

METODOLOGIE E STRATEGIE:
Il percorso proposto si basa su un approccio sia quantitativo sia qualitativo alla probabilità, coinvolgendo la nozione di frequenza. La psicologia cognitiva suggerisce il termine frequenza naturale (Hoffrage et al., 2002) per indicare un rapporto non espresso da frazioni o percentuali, ma descritto attraverso situazioni concrete, che coinvolga un’azione di estrazione o suddivisione e sia dunque intuitivo. L’uso di frequenze naturali in combinazione con materiali pratici e coinvolgenti rende accessibili agli studenti della scuola primaria concetti e contenuti probabilistici (Till e Sproesser, 2020). Questo consente un successivo passaggio verso l’astrazione e il concetto di frazione.

COLLEGAMENTI INTERDISCIPLINARI:

Il percorso è stato ideato da Luigi Bernardi, Dario Domingo.

Acharya Pingala

Pingala è stato un poeta e matematico indiano. Di lui si sa poco, sappiamo che è nato in India, ma non in quale città. Si è però tramandata una sua opera, la Chandahśāstra, in cui emergono le sue doti di poeta e di matematico: infatti Pingala analizza matematicamente la poesia sanscrita, l’antica lingua indiana. Si tratta di fatto di uno dei primi trattati di combinatoria, completo e chiaro grazie ai numerosi esempi. Troviamo non solo i primi spunti di calcolo combinatorio, ma anche di scrittura binaria, della successione di Fibonacci e dell’uso dello zero. Più precisamente, Pingala studia l’alternarsi di sillabe corte (tipo “a”) e sillabe lunghe (tipo “atà”): indica con 1 le sillabe lunghe e con 0 quelle corte, e traduce quindi un verso in una successione di 0 e 1. Per esempio, un verso di 6 sillabe il cui suono è del tipo a-a-atà-a-a-atà corrisponde a 001001. Se un verso ha n sillabe, le possibili successioni sono 2n, e ciascuna di esse corrisponde alla scrittura binaria di un numero. Anche per questo motivo i soldi finti del nostro percorso richiamano proprio le potenze di 2.
Consideriamo ora che una sillaba corta C (cioè “a”) è fatta di una battuta, mentre un sillaba lunga L (cioè “atà”) è fatta di due battute. Allora in una battuta può starci solo una sillaba corta C (1 possibilità), in 2 battute ci possono stare due sillabe corte CC o una sillaba lunga L (2 possibilità), in tre battute ci possono stare CCC, CL e LC (3 possibilità), in quattro battute ci possono stare CCCC, LL, CCL, LCC, CLC (5 possibilità). Sorprendentemente, i numeri di possibilità che abbiamo trovato (1, 2, 3, 5, …) corrispondono esattamente ai numeri di Fibonacci; in particolare, ogni numero è somma dei due numeri che lo precedono. Pingala studia poi quante delle successioni di n sillabe hanno un certo numero k di sillabe corte, trovando quelli che oggi chiamiamo coefficienti binomiali, cioè i numeri che compaiono nel triangolo di Tartaglia, che i francesi chiamano triangolo di Pascal e gli indiani triangolo di Halayudha, un matematico del 10° secolo che scrisse un commento alla Chandaḥśāstra di Pingala!