Il gioco online PITAGORAS GAME, che accompagna le varie attività, è un gioco sul calcolo mentale.



Scheda Tecnica
CLASSI: prima, seconda, terza, quarta e quinta.
Competenze Indicazioni Nazionali:
L'alunno:
- si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali;
- riesce a risolvere facili problemi in tutti gli ambiti di contenuto, mantenendo il controllo sia sul processo risolutivo sia sui risultati;
- descrive il procedimento seguito e riconosce strategie di soluzione diverse dalla propria.
METODOLOGIE E STRATEGIE:
Partendo da attività relative all'addizione e alla moltiplicazione, il percorso ha l'obiettivo di favorire lo sviluppo del senso del numero e promuovere il calcolo mentale. Diverse ricerche sottolineano infatti l'importanza del calcolo mentale non solo per la comprensione dell'aritmetica, ma anche per favorire il passaggio da uno schema additivo ad uno moltiplicativo, promuovendo una migliore concettualizzazione del numero. Il calcolo mentale richiede una certa agilità mentale: bisogna essere capaci di cambiare strategia in corso d'opera, di accettare l'errore come parte del processo e di concentrarsi sul “qui e ora”. Questa dimensione suggerisce l'efficacia di contesti didattici in cui gli studenti calcolano e si descrivono a vicenda come hanno fatto i loro calcoli. In questo processo, l'insegnante ha un ruolo chiave: mette in evidenza connessioni e proprietà, valorizza i diversi approcci con un linguaggio chiaro e propone strumenti per la registrazione condivisa delle strategie.
Esistono almeno quattro buoni motivi per insegnare calcolo mentale (Threlfall, 2002): è il tipo di calcolo più usato nella vita quotidiana; favorisce lo sviluppo del senso del numero; potenzia le abilità di problem-solving; e costituisce una base solida per l'apprendimento del calcolo scritto. È inoltre opportuno che gli studenti si abituino a eseguire i calcoli senza un ausilio scritto, perché le strategie in atto quando si calcola su carta sono diverse da quelle del calcolo mentale.
Il percorso è stato ideato da Luigi Bernardi, Giorgia Damiano.
Il gioco online PITAGORAS GAME, che accompagna le varie attività, è un gioco sul calcolo mentale.




-
attività
- Guida alle OILERCARDS
- L'addizione e la moltiplicazione con il POP IT
- Pari e dispari
- La moltiplicazione
- Il decanomio
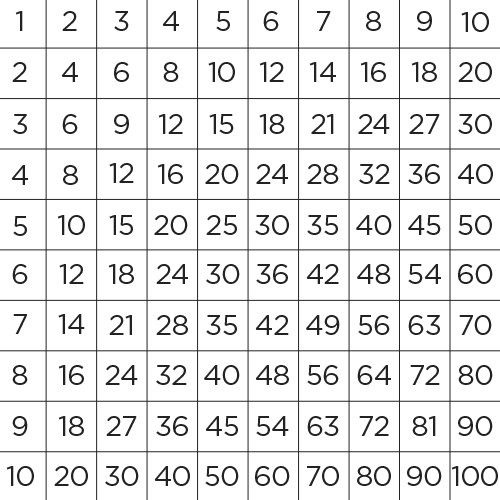
- La tavola pitagorica I
- La tavola pitagorica II
- Calcoli a mente I
- Calcoli a mente II
- Calcoli a mente III
- I numeri triangolari
- I numeri negativi
- Le potenze
- Decine e unità
Scheda Tecnica
CLASSI: prima, seconda, terza, quarta e quinta.
Competenze Indicazioni Nazionali:
L'alunno:
- si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali;
- riesce a risolvere facili problemi in tutti gli ambiti di contenuto, mantenendo il controllo sia sul processo risolutivo sia sui risultati;
- descrive il procedimento seguito e riconosce strategie di soluzione diverse dalla propria.
METODOLOGIE E STRATEGIE:
Partendo da attività relative all'addizione e alla moltiplicazione, il percorso ha l'obiettivo di favorire lo sviluppo del senso del numero e promuovere il calcolo mentale. Diverse ricerche sottolineano infatti l'importanza del calcolo mentale non solo per la comprensione dell'aritmetica, ma anche per favorire il passaggio da uno schema additivo ad uno moltiplicativo, promuovendo una migliore concettualizzazione del numero. Il calcolo mentale richiede una certa agilità mentale: bisogna essere capaci di cambiare strategia in corso d'opera, di accettare l'errore come parte del processo e di concentrarsi sul “qui e ora”. Questa dimensione suggerisce l'efficacia di contesti didattici in cui gli studenti calcolano e si descrivono a vicenda come hanno fatto i loro calcoli. In questo processo, l'insegnante ha un ruolo chiave: mette in evidenza connessioni e proprietà, valorizza i diversi approcci con un linguaggio chiaro e propone strumenti per la registrazione condivisa delle strategie.
Esistono almeno quattro buoni motivi per insegnare calcolo mentale (Threlfall, 2002): è il tipo di calcolo più usato nella vita quotidiana; favorisce lo sviluppo del senso del numero; potenzia le abilità di problem-solving; e costituisce una base solida per l'apprendimento del calcolo scritto. È inoltre opportuno che gli studenti si abituino a eseguire i calcoli senza un ausilio scritto, perché le strategie in atto quando si calcola su carta sono diverse da quelle del calcolo mentale.
Il percorso è stato ideato da Luigi Bernardi, Giorgia Damiano.
Pitagora di Samo
 I racconti sulla vita di Pitagora sono un misto di leggenda e di realtà. Nulla è certo, perché non ha lasciato scritti, ma diverse informazioni sono state tramandate e ci sono pervenute attraverso i suoi discepoli, e alcuni scritti di Aristotele, Erodoto e Platone. Così sappiamo che visse nel 6° secolo a. C., che nacque in Grecia ma viaggiò molto, fra Asia Minore e Egitto (si narra che fu Talete a illustrargli le conoscenze matematiche dell’Oriente), prima di arrivare in Italia, a Crotone, dove fondò una Scuola, cioè una comunità scientifico-filosofico-religiosa i cui discepoli rispettavano determinate regole morali e si impegnavano a non divulgare le conoscenze filosofiche e matematiche che avevano appreso dal maestro Pitagora.
I racconti sulla vita di Pitagora sono un misto di leggenda e di realtà. Nulla è certo, perché non ha lasciato scritti, ma diverse informazioni sono state tramandate e ci sono pervenute attraverso i suoi discepoli, e alcuni scritti di Aristotele, Erodoto e Platone. Così sappiamo che visse nel 6° secolo a. C., che nacque in Grecia ma viaggiò molto, fra Asia Minore e Egitto (si narra che fu Talete a illustrargli le conoscenze matematiche dell’Oriente), prima di arrivare in Italia, a Crotone, dove fondò una Scuola, cioè una comunità scientifico-filosofico-religiosa i cui discepoli rispettavano determinate regole morali e si impegnavano a non divulgare le conoscenze filosofiche e matematiche che avevano appreso dal maestro Pitagora.
Tutti conoscono il Teorema di Pitagora, ma in realtà alla base della dottrina pitagorica non c’era la geometria ma l’aritmetica. Sull’aritmetica si fondavano le altre discipline da cui era composta la matematica: musica, geometria, astronomia. Il numero, infatti, era per Pitagora l’essenza di tutte le cose. La conoscenza delle proprietà dei numeri interi faceva parte di un percorso mistico. Assumevano importanza particolari rappresentazioni come quelle dei numeri triangolari o piramidali.
Sembra che la scuola pitagorica sia stata messa in crisi dalla scoperta dei numeri irrazionali, o meglio, dal fatto che il rapporto fra la diagonale e il lato di un quadrato non si potesse esprimere come rapporto fra numeri interi. Ma questa è un’altra storia...